提到“勾股定理”很多人都知道,但是說到畢達哥拉斯定理有人就不知道了,其實,畢達哥拉斯定理又稱為勾股定理也叫百牛定理,你知道這是為什么嗎?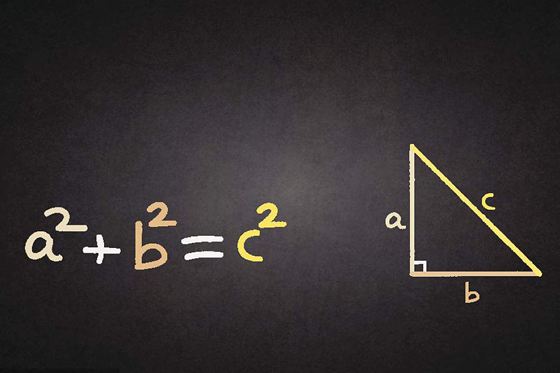 為什么畢達哥拉斯定理又稱為勾股定理? 在平面幾何中,有這樣一條著名的定理:直角三角形中,兩直角邊的平方和等于斜邊的平方,即c²=a²+b²。西方人認為這定理是畢達哥拉斯在公元前500年發現的,所以稱為畢達哥拉斯定理。為了慶祝這一定理的發現,畢達哥拉斯學派殺了一百頭牛酬謝供奉神靈,因此這個定理又有人叫做“百牛定理”。 其實在我國現存最早的數學著作《周髀算經》上,記載了公元前六七世紀榮方和陳子有關這條定理的一段對話,陳子說:“若求邪(斜)……勾股各自乘,并而開方除之”。這段話用公式表示即為:C等于根號下A平方加上B平方或C平方等于A平方加上B平方。因為陳子是比畢達哥拉斯早年代的人,所以有人主張將 “畢達哥哥拉斯定理”改稱“陳子定理”。1951年,我國的《中國數學》雜志以“勾股定理”為其命名。  畢達哥拉斯定理是如何發現的?(故事) 畢達哥拉斯有次應邀參加一位富有政要的餐會,這位主人豪華宮殿般的餐廳鋪著是正方形美麗的大理石地磚,由于大餐遲遲不上桌,這些饑腸轆轆的貴賓頗有怨言;但這位善于觀察和理解的數學家卻凝視腳下這些排列規則、美麗的方形磁磚,但畢達哥拉斯不只是欣賞磁磚的美麗,而是想到它們和"數"之間的關系,于是拿了畫筆并且蹲在地板上,選了一塊磁磚以它的對角線AB為邊畫一個正方形,他發現這個正方形面積恰好等于兩塊磁磚的面積和。他很好奇,于是再以兩塊磁磚拼成的矩形之對角線作另一個正方形,他發現這個正方形之面積等于5塊磁磚的面積,也就是以兩股為邊作正方形面積之和。至此畢達哥拉斯作了大膽的假設: 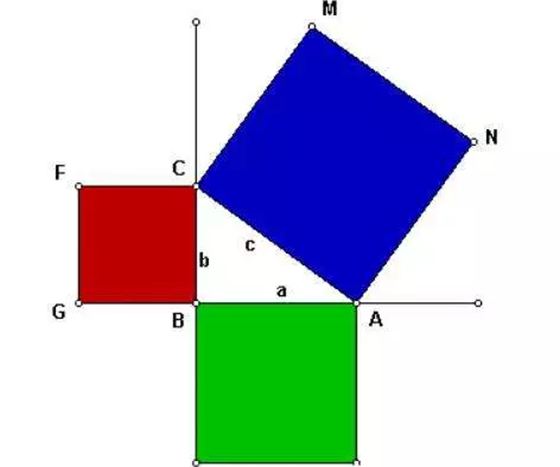 勾股定理的意義 1、勾股定理是聯系數學中最基本也是最原始的兩個對象——數與形的第一定理。 2、勾股定理導致不可通約量的發現,從而深刻揭示了數與量的區別,即所謂“無理數"與有理數的差別,這就是所謂第一次數學危機。 3、勾股定理開始把數學由計算與測量的技術轉變為證明與推理的科學。 4、勾股定理中的公式是第一個不定方程,也是最早得出完整解答的不定方程,它一方面引導到各式各樣的不定方程,另一方面也為不定方程的解題程序樹立了一個范式。 |


